Das Pascalsche Dreieck

Das Pascalsche Dreieck dient zur Lösung von Binomischen Formeln. Binomische Formeln sind zum Beispiel:

(a+b)2 = a2 + 2ab + b2

(a+b)3 = a3 + 3a2b + 3ab2 + b3

(a-b)1 = a - b



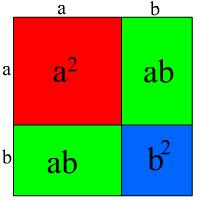
Verallgemeinert also: (a+b)n, wobei a und b auch negativ sein können. Um (a+b)2 auszurechnen, kann man entweder (a+b)(a+b) durchmultiplizieren, oder es sich durch ein Quadrat mit der Seitenlänge a+b veranschaulichen:



Heraus kommt also: a2 + 2ab + b2.

Für (a+b)3 ist auch eine graphische Lösung möglich: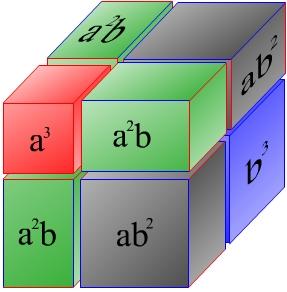


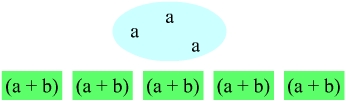
-> Darstellung ohne JS


Es kommt a3 + 3a2b + 3ab2 + b3 heraus.
Wenn man nun (a+b)4 rechnen will, müsste man einen sogenannten 4-Dimensionalen Hyperwürfel zeichnen oder durchmultiplizieren. Für einen Menschen ist ein Hyperwürfel nicht vorstellbar, und durchmultiplizieren wäre sehr ineffizient. Nun kommt einem die Kombinatorik zu Hilfe. (a+b)n ist gleichbedeutend mit:

(a+b)(a+b)(a+b)...


Beim durchmultiplizieren nimmt man die erste Klammer und löst sie auf:

a(a+b)(a+b)... + b(a+b)(a+b)...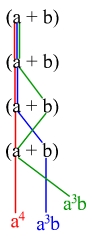


So geht man mit allen weiteren Klammern auch vor. Das kann man sich so veranschaulichen:



Wenn man die ausgewählten Summanden (a oder b) jeder Klammer der Reihe nach aufschreibt, erhät man für die rote Linie a-a-a-a, für die blaue a-a-a-b und für die grüne a-a-b-a. Das erinnert an das Zählen im Binärsystem. Es werden also alle Möglichkeiten einzeln durchgearbeitet. Davon gibt es 2n. Manchmal kommt, wie im Beispiel blau und grün, eine Kombination von Buchstaben öfter vor. Jetzt kann man ausrechnen, wie oft sie vorkommt, indem man die Kombinatorik anwendet.
Wie oft kommt also a3b2 in (a+b)5 vor? (Die Summe der Exponenten der Summanden des Ergebnisses ist übrigens immer gleich dem Exponenten des Binoms.)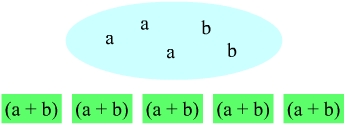



Wie viele Möglichkeiten gibt es also, die Elemente aus dem blauen Bereich denen aus dem grünen zuzuordnen? Wenn alle a-Elemente zugeordnet sind, ergeben sich die Plätze für die b-Elemente automatisch. Also müssen wir nur die Anzahl der möglichen Zuordnungen der a-Elemente ausrechnen:



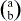Das geht mit einer sogenannten Kombination. Die Schreibweise ist Zwei übereinanderstehende Werte in einer Klammer; oben a und unten b., gesprochen "Kombination von a Elementen zur b-ten Klasse" und damit kann man ausrechnen, wie viele Möglichkeiten es gibt, jeweils b Elemente von a zusammenzufassen.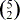
Beispiel:
Wenn von 5 Personen jeder jedem die Hand schütteln will, wie viele Begegnungen muss es geben?
Lösung: Oben 5, unten 2.

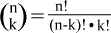
Errechnen lässt sich eine Kombination durch Oben n, unten k = (n!)/((n-k)! * k!)
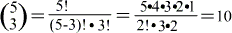
Im Beispiel müssen wir 5 Elemente zur 3-ten Klasse kombinieren: Oben 5, unten 3 = (5!)/((5-3)! * 3!) = 10
Der Summand a3b2 kommt also 10 mal vor, darum steht in der Lösung des Binoms 10a3b2.

Allgemeiner:
    Den Koeffizienten des Summanden akbn-k der Lösung des Binoms (a+b)n errechnet man durch 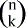Kombination von n elementen zur k-ten Klasse.

Nun wird ein Dreieck (oder genau gesagt Eineck, weil es unendlich weit nach unten weitergeht) aufgestellt, und zwar so, dass nach unten der Exponent des Binoms wächst, und nach links der Exponent von dem a von (a+b)n zunimmt, und nach rechts Exponent von dem b von (a+b)n zunimmt.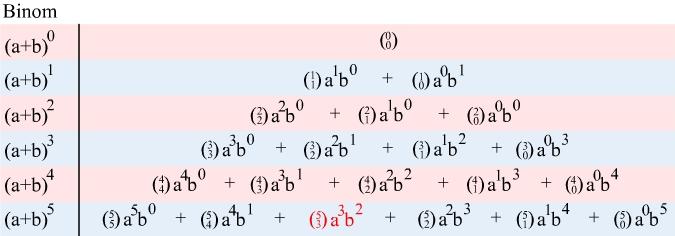


Zur Übersicht rechnet man die Koeffizienten aus und schreibt nur sie in die Tabelle:

Exponent                        
0             1          
1           1   1        
2         1   2   1      
3       1   3   3   1    
4     1   4   6   4   1  
5   1   5   10   10   5   1


Das nennt man das Pascalsche Dreieck. Es fällt auf, dass eine Zahl immer die Summe der oberen beiden Zahlen ist. Die Zehn aus dem Beispiel, die hier rot gefärbt ist, ist zum Beispiel die Summe von den darüberliegenden Zahlen 4 und 6. Das kann man durch die Kombinationsschreibweise und deren Formel leicht beweisen:
Wir nehmen wieder unsere rote Beispielzahl und den dazu passenden Ausschnitt aus dem Dreieck:
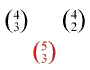
Kombination von 5 Elementen zur 3-ten Klasse; drüber links: 4 zur 3. Klasse, drüber rechts 4 zur 2. Klasse

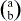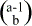Der Wert links über Kombination von a Elementen b ten Klasse. ist also Kombination von a-1 Elementen b ten Klasse., und rechts darüber ist 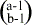Kombination von a-1 Elementen b-1 ten Klasse.. Nun wird daraus eine Gleichung gemacht:



Heraus kommt also eine wahre Aussage. Damit ist der Beweis fertig.

Eine interessante Seite zum Pascalschen Dreieck ist www.arndt-bruenner.de/mathe/scripts/pascalmod.htm.


Verallgemeinerung zum Pascalschen Tetraeder