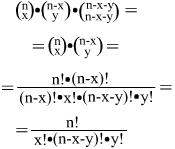Der Pascalsche Tetraeder
Um "trinomische" Formeln lösen zu können, kann man die Erweiterung der binomischen Formeln benutzen:
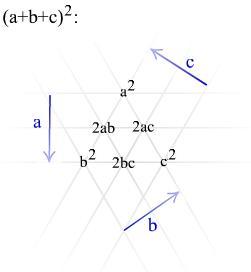
(a+b+c)2 =
= ((a+b)+c)2 =
= (a+b)2 + 2(a+b)c + c2 =
= a2 + 2ab + b2 + 2ac + 2bc + c2 =
= a2 + b2 + c2 + 2ab + 2ac + 2bc
Ein weiteres Beispiel ist eine trinomische Formel mit dem Exponenten 3:
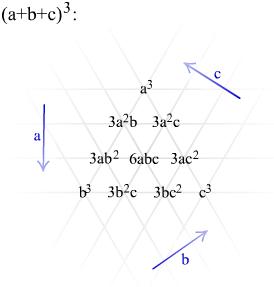
(a+b+c)3 =
= ((a+b)+c)3 =
= (a+b)3 + 3(a+b)2c + 3(a+b)c2 + c3 =
= a3 + 3a2b + 3ab2 + b3 + 3c(a2+2ab+b2) + 3ac2 + 3bc2 + c3 =
= a3 + 3a2b + 3ab2 + b3 + 3a2c + 6abc + 3b2c + 3ac2 + 3bc2 + c3 =
= a3 + b3 + c3 + 3a2b + 3ab2 + 3a2c + 3b2c + 3ac2 + 3bc2 + 6abc
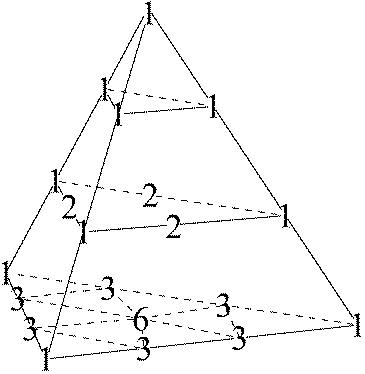
Die Summanden der Lösung kann man immer so anordnen:
oder
Zur Pfeilspitze hin nimmt der Exponent des entsprechenden Faktors immer ab. Bei der Koeffizientenberechnung kommt einem wieder die Kombinatorik zu Hilfe. Man muss auf der einen Seite wieder die Faktoren anordnen und auf der anderen die Klammern. Als Beispiel berechnen wir den Koeffizienten vom Summanden abc2 aus der Lösung des Trinoms (a+b+c)4:
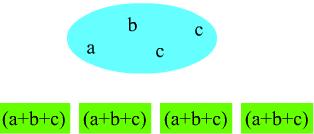
Wieviele Möglichkeiten gibt es hier, die Buchstaben aus dem blauen Bereich den grünen Kästen zuzuordnen? Um das a zuzuordnen, gibt es 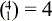 Möglichkeiten. Dann sind noch 3 grüne Kästen frei. Wieviele Möglichkeiten gibt es nun noch, das b zuzuordnen?
Möglichkeiten. Dann sind noch 3 grüne Kästen frei. Wieviele Möglichkeiten gibt es nun noch, das b zuzuordnen? 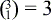 . Die Plätze für die Ces ergeben sich nun automatisch. Insgesamt sind es also
. Die Plätze für die Ces ergeben sich nun automatisch. Insgesamt sind es also 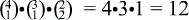 Möglichkeiten.
Möglichkeiten.
Allgemein lässt sich der Koeffizient vom Summanden axbycn-x-y der Lösung des Trinoms (a+b+c)n so berechnen:
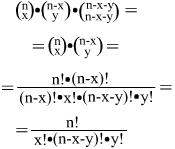
Wenn man die Lösungsdreiecke übereinander legt, ergibt sich ein Tetraeder(oder "Monoeder", weil er unendlich weit fortgesetzt werden kann):




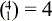 Möglichkeiten. Dann sind noch 3 grüne Kästen frei. Wieviele Möglichkeiten gibt es nun noch, das b zuzuordnen?
Möglichkeiten. Dann sind noch 3 grüne Kästen frei. Wieviele Möglichkeiten gibt es nun noch, das b zuzuordnen? 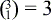 . Die Plätze für die Ces ergeben sich nun automatisch. Insgesamt sind es also
. Die Plätze für die Ces ergeben sich nun automatisch. Insgesamt sind es also 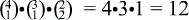 Möglichkeiten.
Möglichkeiten.